IDEA
이 논문은 Siamese Neural Networks을 사용하여 레시피를 학습하고 새로운 조합을 추천해주는 모델이다. Siamese Neural Networks은 클래스간 여러조합의 Pair를 만들고 같은 Network를 통해 fully conntected netowrk를 만든다. 하지만, 마지막 output에서 2개 결과간의 distance를 구하여 학습하도록 한다. label데이터가 아니라 Pair로 된 데이터가 서로에게 label되어 같은 class인지 아닌지를 확인시켜주기 때문에 기존에 학습되어있지 않은 데이터가 들어오더라도 분류할 수 있고, 데이터 셋에 기존에 Pair로 되어있지 않아도 충분히 같은 class인지 분류할 수 있다고 생각되어진다. [https://kyounju.tistory.com/48]
이 모델이 Siamese Neural Networks을 통해 하고 싶은것은 하나의 음식에 대한 성분들을 셋을 가지고 이 음식에 속할 수 있는 재료인지 아닌지를 구별하고 싶어한다. 또, 실제로 레시피에 속해있지 않은 성분이 레시피의 일부분이 될 수 있는지 없는지도 알 수 있게 하여 새로운 레시피를 탄생시켜 준다.
DataSet
이 모델은 Recipe1M의 DataSet은 사용하였다. 이 DataSet은 image와 text로 나누어지는데 text를 전처리 하여 사용하였다고 한다. Recipe1M에는 올리브오일 2스푼 이러한 방식으로 데이터가 이루어져 있는것으로 보인다. 하지만 이 모델에서는 word2vec을 통해 feature가 되는 성분들만 뽑아서 사용하였다. 예를 들어 음식마다 올리브 오일이 2스푼 들어가는 것도 있고, 3스푼 들어가는 것도 있지만 text의 feature가 되는 올리브 오일이라는 text만을 성분 추출해서 사용하였다. 결국 완벽한 레시피를 만드는 모델은 아닌것으로 보인다.
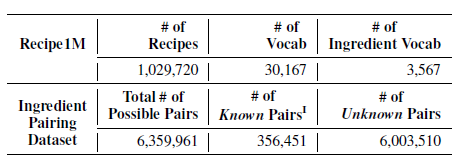
위에 그림에서 보면 레시피 Data들은 10294720이고, 각 성분 30167개이다. word2vec으로 뽑아낸 feature은 3567개이다. 3567개에서 2개씩 추출하여 총 6359961개의 데이터셋을 만들 것이다.
각 Pair의 Score구하기
각 성분에 pair쌍에 대한 score를 co-occurrence matrix만들 것이다.
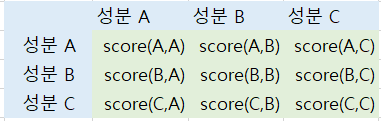
score의 공식은 아래와 같다. 성분 x, 성분 y의 확률 분포 및 조건부 확률을 구하여 아래와 같이 계산하면 된다.
$$ pmi(x;y) = \log \frac {p(x,y)} {p(x)p(y)} $$
하지만, 이 모델은 -1 ~ 1 사이의 값을 갖기 위해 npmi를 사용하였다고 한다.
$$ npmi(x; y) = \log \frac {pmi(x;y)} {h(x,y)},\\ h(x,y) = -\log {p(x,y)} $$
데이터상 성분의 개수가 20개 이하인것, 매트릭스에서 성분의 쌍이 5개 이하인것은 noise로 취급하여 제거하고 사용하였다고 한다.
Model

네트워크를 크게 deep layer와 wide layer 2가지 로 구분 할 수 있다. MLP를 지나간 2개의 fully connected layer를 concat하여 한개의 matrix로 만들어준다. deep layer는 Siamese Neural Networks의 ouput을 가지고 한번더 MLP를 지나가게 하여 encoding시킨다. layer한개는 ReLu를 가진 신경망이다.
$$ h_{l} = f(W_{l}X_{l-1} + b_{l}),\ \ \ f(\cdot) = max(0, v)$$
Siamese Neural Networks네트워크에서 결과물인 fully connected layer 2개를 concat하여 하나의 matrix로 합친다. deep layer에는 concat을 input으로 넣고 결과물로 만들고, wide layer에는 concat과 deep layer의 결과물 다시 한번 concat한다. 마지막 concat을 통해 score를 아래와 같이 계산한다.
$$ Y_{ab} = W_{l}(w,d) + b_{l} $$
Train
Loss function으로는 mean squared error를 사용한다.
$$ L = \sum (y_{ab} - Y_{ab})^2 $$
나의 결론
흥미로운 논문인거 같아서 읽어봤지만, 일단 양의 정보가 빠진 재료의 명만 가지고 있어 완벽하다고 생각하진 않는다. 또, 결국 2개 쌍의 socre로 어울리는지 안어울리는 판단해야 하는데, 음식에는 재료가 무수하게 들어간다. 하지만, 2가지가 어울린다고 전체적인 음식의 맛이 좋을거라고 생각하는건 greedy algorithm같은 오류에 빠진 생각이 아닐까? 만약 실제로 이 모델로 음식을 만들것이라면 2가지 음식사이의 score가 높으면 모든 재료를 사용한 음식의 score도 높다라는 것을 증명해야만 할 것이다.
댓글